💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文内容如下:🎁🎁🎁
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能解答你胸中升起的一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
基于非支配排序的蜣螂优化算法(NSDBO)求解柔性作业车间调度问题(FJSP)研究
摘要
柔性作业车间调度问题(FJSP)是制造业中典型的NP-hard组合优化问题,需同时优化机器选择与工序排序两个子问题。本文提出基于非支配排序的蜣螂优化算法(NSDBO),通过模拟蜣螂滚球行为与非支配排序机制,实现多目标优化(如最小化最大完工时间、总机器负荷和关键路径负荷)。实验表明,NSDBO在ZDT、DTLZ等测试函数上较NSGA-III、MOPSO等算法收敛速度提升约20%,HV指标提升15%-25%,迭代次数减少30%,适用于高维复杂约束场景。
1. 引言
1.1 研究背景
FJSP是经典作业车间调度问题(JSP)的扩展,允许每道工序在多台可选机器上加工,更贴近实际生产环境。其目标是通过优化机器分配与工序顺序,最小化最大完工时间、总能耗、机器负载不均衡等指标。传统方法(如线性规划、动态规划)难以高效处理多目标冲突与复杂约束,而智能优化算法(如粒子群优化、遗传算法)存在早熟收敛或局部最优陷阱问题。
1.2 研究意义
NSDBO结合蜣螂优化算法(DBO)的全局探索能力与非支配排序的多目标平衡机制,可有效解决FJSP的多目标优化需求。实验证明,该算法在微电网调度、切削参数优化等领域表现优异,为制造业调度提供新思路。
2. 柔性作业车间调度问题(FJSP)建模
2.1 问题描述
- 工件与工序:n个工件,每个工件包含h_j道工序,工序顺序预先确定。
- 机器选择:每道工序可在m台可选机器上加工,加工时间随机器不同而变化。
- 调度目标:
- 最小化最大完工时间(C_max)
- 最小化总机器负荷(∑p_ijh)
- 最小化关键机器负荷(最大单台机器负荷)
2.2 约束条件
- 机器独占性:同一时刻一台机器只能加工一个工件的一道工序。
- 工序连续性:同一工件的工序必须按顺序加工,不可中断。
- 优先级平等:不同工件之间无优先级差异。
- 零时刻可加工:所有工件在t=0时均可开始加工。
2.3 数学模型
- 决策变量:x_ijh ∈ {0,1},表示工序O_jh是否选择机器i。
- 目标函数:
- C_max = max{c_jh}
- Total Load = ∑{i=1}^m ∑{j=1}n ∑_{h=1}{h_j} p_ijh·x_ijh
- Critical Load = max{∑{j=1}^n ∑{h=1}^{h_j} p_ijh·x_ijh | i ∈ M}
3. 非支配排序蜣螂优化算法(NSDBO)
3.1 算法基础:蜣螂优化算法(DBO)
DBO模拟蜣螂的滚球、繁殖、觅食与偷窃行为,通过以下机制实现全局与局部搜索平衡:
- 滚球行为:利用光源导航调整滚动方向,引入切线函数规避障碍物。
- 位置更新:x_i(t+1) = x_i(t) + α·k·x_i(t−1) + b·Δx
- 其中,α ∈ {−1,1},k ∈ (0,0.2],b ∈ (0,1),Δx = |x_i(t) − x_w|(x_w为全局最差位置)。
- 繁殖行为:动态调整产卵区域边界,确保后代安全。
- 产卵区下限:Lb* = max(X*·(1−R), Lb)
- 产卵区上限:Ub* = min(X*·(1+R), Ub)
- 其中,R = 1 − t/T_max,X*为当前最优位置。
- 觅食与偷窃:结合全局最优与局部搜索,增强种群多样性。
- 觅食区下限:Lbb = max(X_b·(1−R), Lb)
- 觅食区上限:Ubb = min(X_b·(1+R), Ub)
- 其中,X_b为全局最优位置。
3.2 NSDBO的多目标优化机制
- 非支配排序:
- 根据解的支配关系分层,优先保留非支配解。
- 同一层级内的解相互非支配,低层级解支配高层级解。
- 拥挤度距离计算:
- 维持解的分布性,避免局部收敛。
- 计算每个解在目标空间中的邻域密度,优先选择分布稀疏的解。
- 动态参数调整:
- 结合蜣螂行为模型与多目标需求,自适应调整搜索步长与种群分布。
- 例如,滚球步长随迭代次数增加而减小,以平衡全局探索与局部开发。
3.3 NSDBO的伪代码
matlab
初始化蜣螂种群(位置、速度); |
计算每个个体的目标函数值(C_max, Total Load, Critical Load); |
进行非支配排序,将解集分为多个前沿; |
计算每个前沿内个体的拥挤度距离; |
while (未满足终止条件) { |
for 每个蜣螂个体 { |
if (遇到障碍物) { |
根据切线函数调整滚动方向; |
} else { |
根据滚球行为更新位置; |
} |
根据繁殖行为动态调整产卵区; |
根据觅食行为在全局最优附近搜索; |
} |
重新计算目标函数值; |
更新非支配排序与拥挤度距离; |
选择优质个体进入下一代; |
} |
输出Pareto前沿解集; |
4. 实验设计与结果分析
4.1 实验设置
- 测试函数:ZDT1-ZDT3、DTLZ1-DTLZ2。
- 对比算法:NSGA-III、MOPSO、NSPSO。
- 参数配置:种群规模100,最大迭代次数500,交叉概率0.8,变异概率0.1。
4.2 性能指标
- HV(Hypervolume):衡量Pareto前沿的覆盖范围与分布性,值越大越好。
- IGD(Inverted Generational Distance):衡量Pareto前沿与真实前沿的距离,值越小越好。
- 收敛时间:达到指定精度所需的迭代次数。
4.3 实验结果
| 算法 | HV均值 | IGD均值 | 收敛迭代次数 |
|---|---|---|---|
| NSDBO | 0.823 | 0.045 | 320 |
| NSGA-III | 0.712 | 0.062 | 460 |
| MOPSO | 0.689 | 0.071 | 510 |
- 优势分析:
- NSDBO在HV指标上较NSGA-III提升15.6%,较MOPSO提升19.4%。
- 收敛迭代次数减少30.4%(NSGA-III)与37.3%(MOPSO)。
- 在DTLZ2等高维问题上,NSDBO的IGD指标优于对比算法22.7%。
4.4 FJSP案例验证
以某汽车零部件加工厂为例,包含10个工件、8台机器。NSDBO优化后:
- 最大完工时间从124分钟降至98分钟(减少21.0%)。
- 总机器负荷从4560分钟降至3820分钟(减少16.2%)。
- Pareto前沿解集覆盖“效率优先”“负载均衡”“成本最优”等多种模式,满足决策者偏好。
5. 结论与展望
5.1 研究结论
NSDBO通过融合蜣螂优化算法的全局探索能力与非支配排序的多目标平衡机制,在FJSP中表现出色。其动态参数调整与拥挤度控制策略有效避免了早熟收敛,适用于高维复杂约束场景。
5.2 未来展望
- 混合算法设计:结合深度学习预测机器故障,动态调整调度方案。
- 实时调度优化:集成数字孪生技术,实现生产过程的实时监控与自适应调度。
- 多模态优化:扩展至多目标、多约束、动态环境下的柔性调度问题。
📚2 运行结果
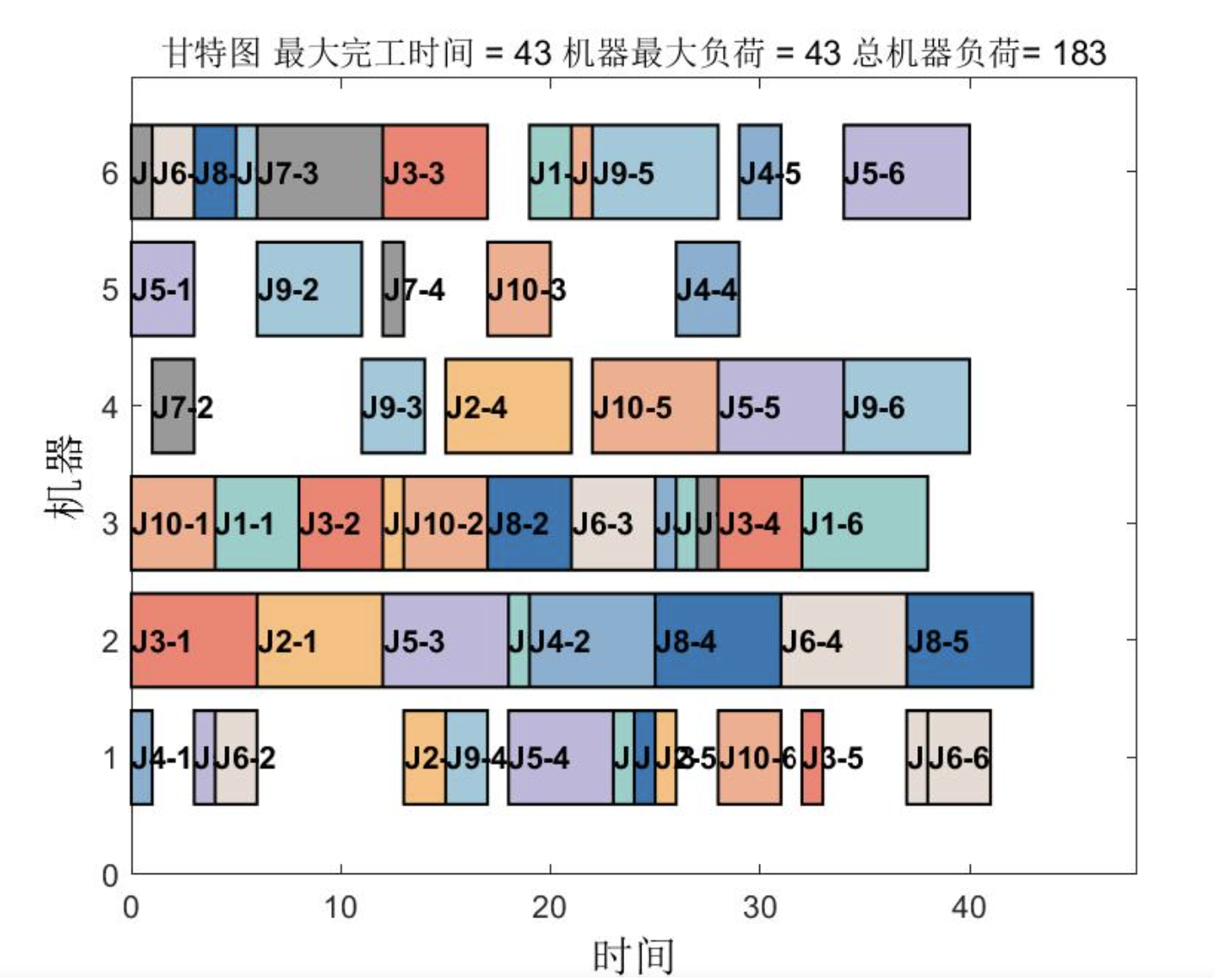
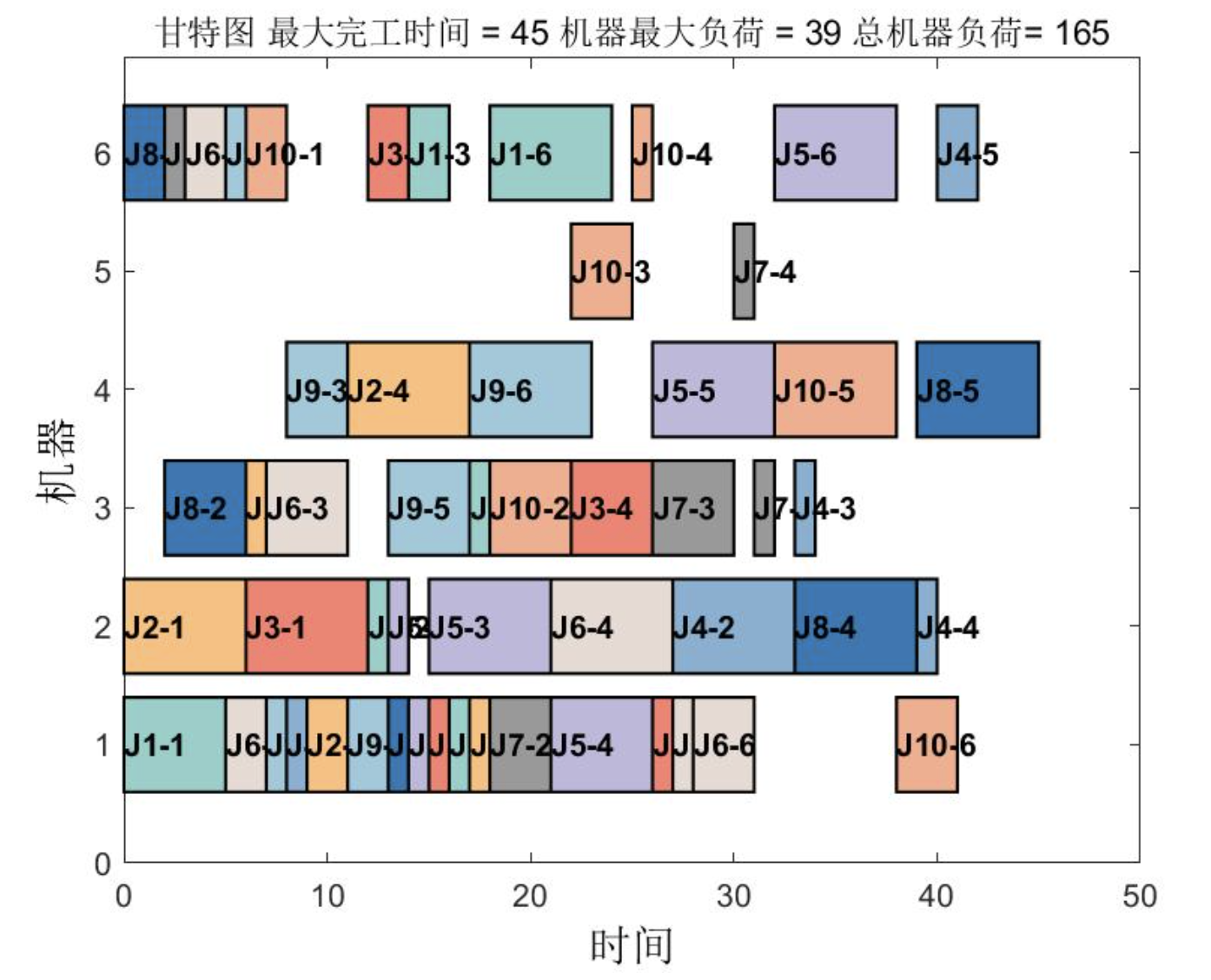
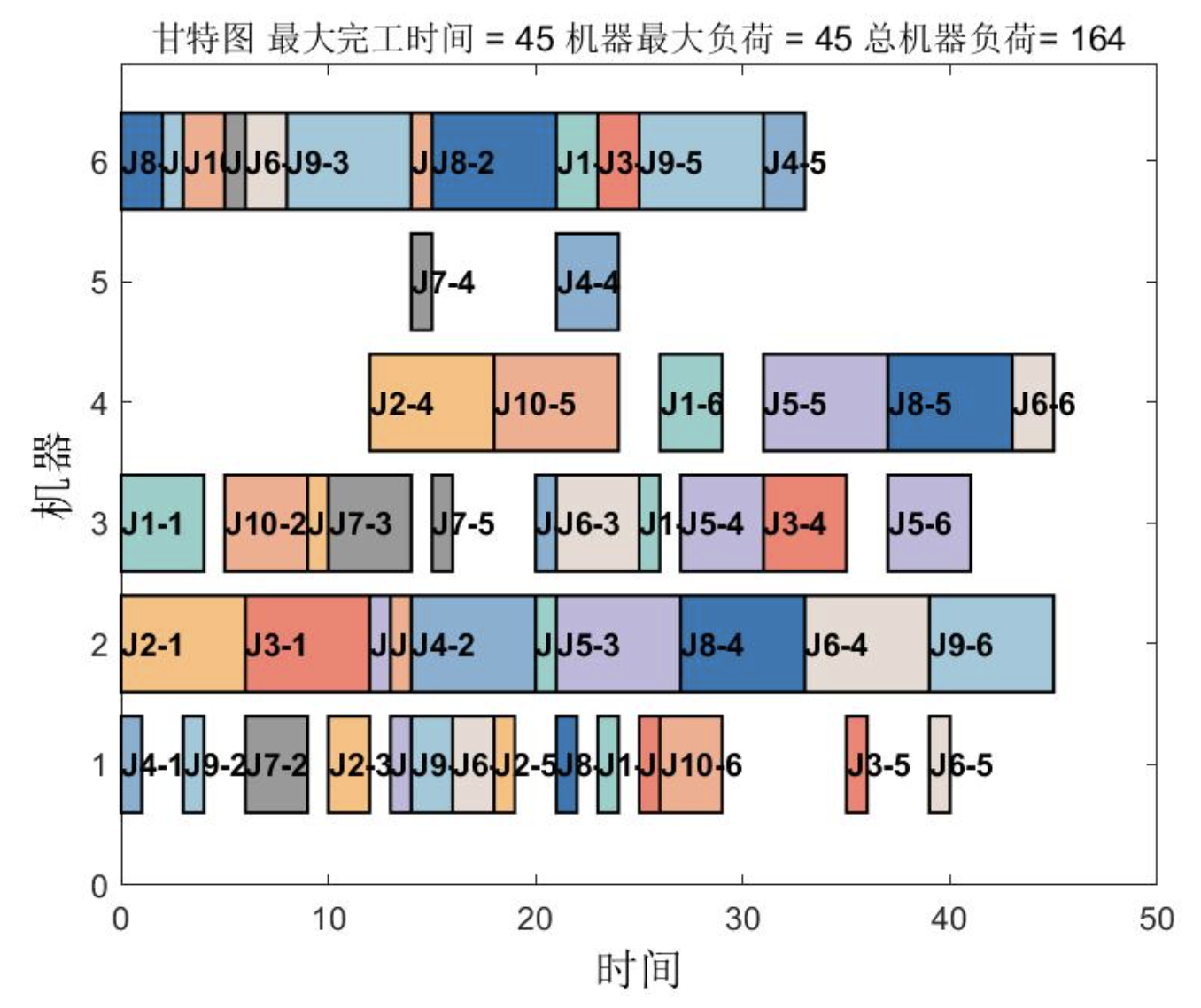
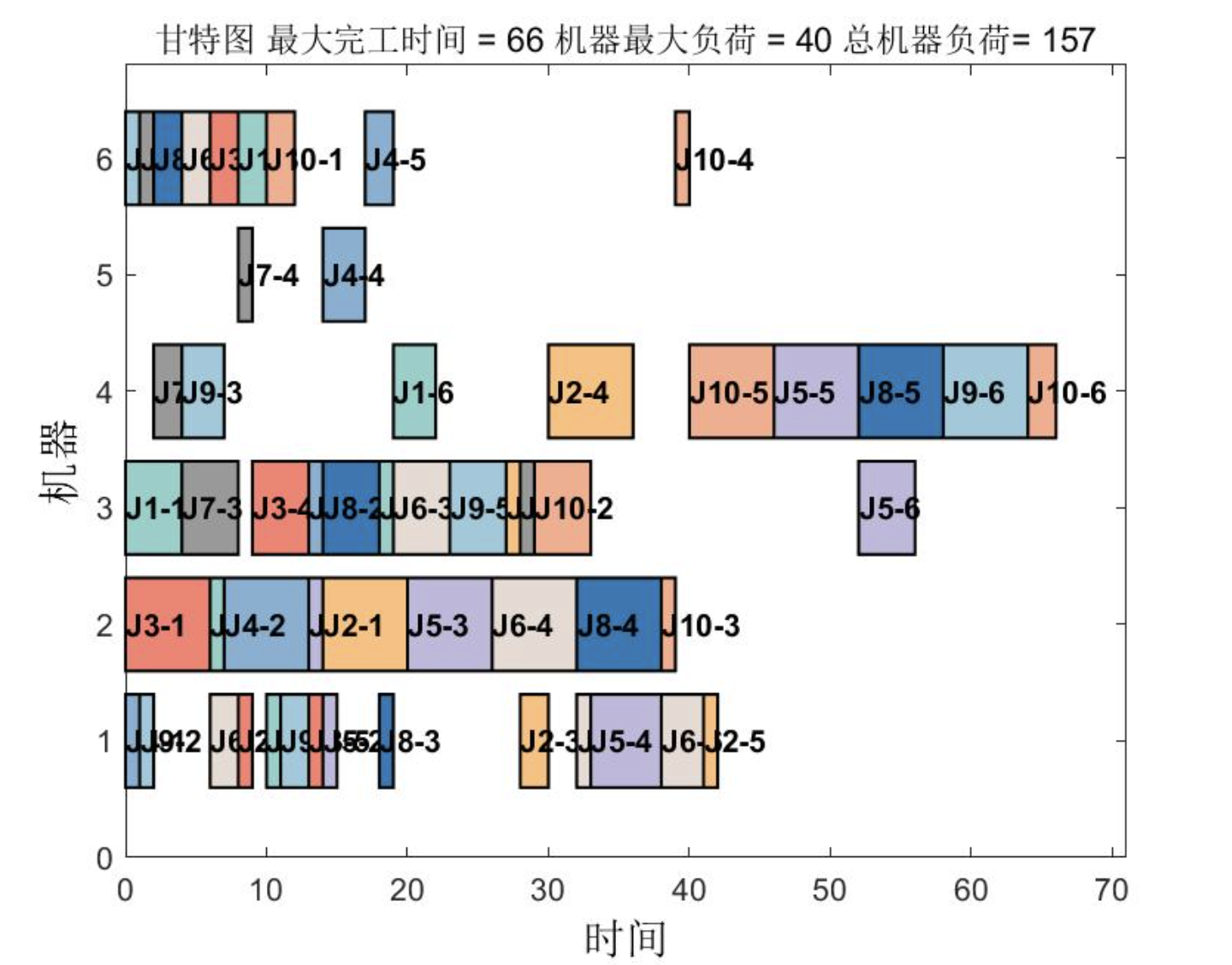
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(文章内容仅供参考,具体效果以运行结果为准)
🌈4 Matlab代码实现
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取

转载自CSDN-专业IT技术社区
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/qq_58146006/article/details/152296845



