一、技术解读

1.1 核心背景与原有痛点

去噪扩散概率模型（DDPM）是生成式AI领域的重要突破，其核心思想模拟了一个"逐步加噪-逐步去噪"的过程。想象一下：将一张清晰图片逐步添加噪声，直到完全变成随机噪点，然后训练神经网络学习如何逆向这个过程，从噪声中重建原图。

然而，原始DDPM存在三大痛点：

• 似然性能不足：虽然生成的图片质量高，但量化指标上不如传统生成模型，让人怀疑其是否真正掌握了数据分布的全貌
• 采样速度极慢：生成一张图片需要数百甚至数千步计算，耗时数分钟，难以实用
• 评估体系不完善：缺乏与GAN在模式覆盖度上的直接对比
• 架构限制：基础网络结构对高多样性数据集适应不足，限制了模型性能的充分发挥

1.2 关键改进技术深度解析

1.2.1 模型架构优化：更强大的特征提取能力

架构基础与创新：
本文在原始DDPM的UNet架构基础上进行了重要改进，构建了更强大的特征提取网络。核心创新包括：

注意力机制增强：

• 采用多头注意力机制（4个注意力头）替代单头注意力
• 在16×16和8×8两个关键分辨率层级都应用注意力，提升全局特征捕获能力
• 注意力计算公式：$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$

条件注入方式革新：

• 时间步信息$t$通过仿射变换注入：GroupNorm(h)(w+1)+b
• 替代原始的加法融合方式GroupNorm(h+v)
• 类别条件信息通过相同路径融入，增强模型表达能力

具体架构配置：

# ImageNet 64×64模型架构
下采样阶段: 4个
每个阶段: 3个残差块
通道配置: [C, 2C, 3C, 4C]  # C=128为基础配置
参数量: ≈1.2亿参数
计算量: 前向传递约390亿FLOPs

1.2.2 智能方差学习：让模型自己决定"去噪步长"

原理解读：
传统的DDPM使用固定方差，就像用固定步长下楼，不够灵活。本文让模型学习每个步骤的最佳方差，相当于让模型自己决定"每一步该走多大"。

技术细节：
方差学习通过以下公式实现：
$${\Sigma }_{\theta }(x_t,t)=\exp (v\log {\beta }_t+(1-v)\log {\tilde{\beta }}_t)$$

这里，$v$是模型学习的参数，${\beta }_t$和${\tilde{\beta }}_t$分别代表方差的上界和下界。这种设计巧妙地将方差约束在合理范围内，避免训练不稳定。

混合损失函数：
$$L_{hybrid}=L_{simple}+\lambda L_{vlb}$$

其中$L_{simple}$确保样本质量，$L_{vlb}$优化对数似然，$\lambda =0.001$平衡两者。这种设计就像"双师教学"，一个老师专攻实践（样本质量），一个老师专攻理论（似然优化）。

1.2.3 余弦噪声调度：更智能的加噪节奏

原理解读：
原始线性调度就像匀速加噪，效率低下。余弦调度模仿"慢-快-慢"的节奏：开始慢慢加噪（保留信息），中间快速破坏，最后缓缓收尾。

数学表达：
$${\bar{\alpha }}_t=\frac{f(t)}{f(0)},f(t)=\cos {\left(\frac{t/T+s}{1+s}\cdot \frac{\pi }{2}\right)}^2$$

其中$s=0.008$确保初始噪声不过小。这种调度使${\bar{\alpha }}_t$曲线更加平滑，避免突变。

1.2.4 重要性采样：优化训练稳定性

原理解读：
不同扩散步的损失值差异巨大，就像班级里学生水平参差不齐。均匀采样会导致"差生"拖累整体进度。重要性采样相当于"因材施教"，给难样本更多关注。

实现方式：
采样概率$p_t\propto \sqrt{E[L_t^2]}$，动态调整以聚焦关键步骤。这显著降低了梯度噪声，使训练更稳定。

1.2.5 快速采样技术：十倍加速的突破

核心洞察：
学习方差后，模型可以用"大跨步"方式采样，而无需小步挪动。从4000步减少到50-100步，实现10-80倍加速。

技术实现：
采样时选择时间步子序列$S$，重新计算对应参数：
$${\beta }_{S_t}=1-\frac{{\bar{\alpha }}_{S_t}}{{\bar{\alpha }}_{S_{t-1}}}$$

学习到的方差${\Sigma }_{\theta }$自动适应不同长度的采样序列，无需重新训练。

1.3 实验验证与性能突破

1. 在ImageNet 64×64数据集上，对数似然从3.99提升至3.53比特/维度，接近传统似然模型水平。这表明DDPM确实能够捕获数据的完整分布。
2. 与BigGAN-deep对比，在相似FID下，DDPM的召回率更高（0.71 vs 0.59），证明其能更好地覆盖数据分布的所有模式，解决了GAN的模式崩溃问题。
3. 模型性能随计算量增加而平稳提升，符合幂律规律。这为后续大规模扩展提供了理论依据。

二、论文翻译： Improved Denoising Diffusion Probabilistic Models（改进的去噪扩散概率模型）

0 摘要

去噪扩散概率模型（DDPM）是一类生成模型，最近已被证明能产生优秀的样本。我们表明，通过一些简单的修改，DDPM 也能实现竞争性的对数似然，同时保持高样本质量。此外，我们发现学习反向扩散过程的方差允许以数量级更少的前向传递进行采样，且样本质量差异可忽略，这对于这些模型的实际部署很重要。我们还使用精确率和召回率来比较 DDPM 和 GAN 覆盖目标分布的程度。最后，我们表明这些模型的样本质量和似然随模型容量和训练计算量平滑缩放，使其易于扩展。我们在 https://github.com/openai/improved-diffusion 发布了代码。

1 引言

Sohl-Dickstein 等人（2015）引入了扩散概率模型，这是一类生成模型，通过学习逆转一个渐进的、多步的加噪过程来匹配数据分布。最近，Ho 等人（2020）展示了去噪扩散概率模型（DDPM）与基于分数的生成模型（Song & Ermon, 2019; 2020）之间的等价性，后者使用去噪分数匹配（Hyvarinen, 2005）学习数据分布的对数密度的梯度。最近已证明这类模型可以产生高质量图像（Ho 等人, 2020; Song & Ermon, 2020; Jolicoeur-Martineau 等人, 2020）和音频（Chen 等人, 2020b; Kong 等人, 2020），但尚未证明 DDPM 能实现与其他基于似然的模型（如自回归模型（van den Oord 等人, 2016c）和 VAE（Kingma & Welling, 2013））竞争的对数似然。这引发了各种问题，例如 DDPM 是否能够捕获分布的所有模式。此外，虽然 Ho 等人（2020）在 CIFAR-10（Krizhevsky, 2009）和 LSUN（Yu 等人, 2015）数据集上展示了极好的结果，但尚不清楚 DDPM 在更高多样性的数据集（如 ImageNet）上的表现如何。最后，虽然 Chen 等人（2020b）发现 DDPM 可以使用少量采样步高效生成音频，但尚未证明对图像也是如此。

在本文中，我们表明 DDPM 可以实现与其他基于似然的模型竞争的对数似然，即使在像 ImageNet 这样的高多样性数据集上。为了更紧密地优化变分下界（VLB），我们使用简单的重参数化和混合学习目标来学习反向过程方差，该目标结合了 VLB 和 Ho 等人（2020）的简化目标。我们惊讶地发现，使用我们的混合目标，我们的模型获得了比直接优化对数似然更好的对数似然，并发现后者的目标在训练期间具有更多的梯度噪声。我们展示了一种简单的重要性采样技术减少了这种噪声，并允许我们实现比混合目标更好的对数似然。

将学习方差纳入模型后，我们惊讶地发现，我们可以用更少的步数从我们的模型中采样，且样本质量变化极小。虽然 DDPM（Ho 等人, 2020）需要数百次前向传递来产生好样本，但我们只需 50 次前向传递就能获得好样本，从而加速采样以用于实际应用。与我们的工作并行，Song 等人（2020a）开发了一种不同的快速采样方法，我们在实验中与他们的方法 DDIM 进行了比较。

虽然似然是与其他基于似然的模型比较的好指标，但我们还想比较这些模型与 GAN 的分布覆盖度。我们使用改进的精确率和召回率指标（Kynkanniemi 等人, 2019），发现扩散模型在相似 FID 下实现了更高的召回率，表明它们确实覆盖了目标分布的更大部分。

最后，由于我们期望机器学习模型在未来消耗更多计算资源，我们评估这些模型在增加模型大小和训练计算量时的性能。类似于（Henighan 等人, 2020），我们观察到趋势表明随着训练计算量的增加，性能有可预测的提升。

2 去噪扩散概率模型

我们简要回顾 Ho 等人（2020）的 DDPM 公式。该公式做了各种简化假设，例如固定的加噪过程 q，它在每个时间步添加对角高斯噪声。更一般的推导见 Sohl-Dickstein 等人（2015）。

2.1 定义

给定数据分布 $x_0\sim q\left(x_0\right)$，我们定义一个前向加噪过程 q，它通过在每个时间步 t 添加方差为 ${\beta }_t\in (0,1)$ 的高斯噪声来产生潜变量 $x_1$ 到 $x_T$，如下：
$$q(x_1,...,x_T\mid x_0):=\prod _{t=1}^{T}q\left(x_t\mid x_{t-1}\right)(1)$$
$$q(x_t\mid x_{t-1}):=\mathcal{N}\left(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I\right)(2)$$
给定足够大的 T 和良好的 ${\beta }_t$ 调度，潜变量 $x_T$ 几乎是各向同性高斯分布。因此，如果我们知道精确的反向分布 $q\left(x_{t-1}\mid x_t\right)$，我们可以采样 $x_T\sim \mathcal{N}(0,I)$ 并反向运行过程以从 $q\left(x_0\right)$ 获取样本。然而，由于 $q\left(x_{t-1}\mid x_t\right)$ 依赖于整个数据分布，我们使用神经网络近似如下：
$$p_{\theta }(x_{t-1}\mid x_t):=\mathcal{N}\left(x_{t-1};{\mu }_{\theta }(x_t,t),{\Sigma }_{\theta }(x_t,t)\right)(3)$$
$q$ 和 $p$ 的组合是一个变分自编码器（Kingma & Welling, 2013），我们可以写出变分下界（VLB）如下：
$$L_{\text{vib}}:=L_0+L_1+\dots +L_{T-1}+L_T(4)$$
$$L_0:=-\log p_{\theta }\left(x_0\mid x_1\right)(5)$$
$$\begin{array}{rl}{L}_{t-1}& :=D_{KL}\left(q\left(x_{t-1}\mid x_t,x_0\right)\mid p_{\theta }\left(x_{t-1}\mid x_t\right)\right)\\ L_T& :=D_{KL}\left(q\left(x_T\mid x_0\right)\mid p\left(x_T\right)\right)\end{array}$$
$$L_T:=D_{KL}\left(q\left(x_T\mid x_0\right)\mid p\left(x_T\right)\right)(7)$$
除了 $L_0$，方程 4 的每一项都是两个高斯之间的 KL 散度，因此可以闭式求解。对于图像的 $L_0$，我们假设每个颜色分量被分成 256 个桶，并计算 $p_{\theta }\left(x_0\mid x_1\right)$ 落在正确桶中的概率（这可以使用高斯分布的 CDF 易处理）。另请注意，虽然 $L_T$ 不依赖于 $\theta$，但如果前向加噪过程充分破坏数据分布使得 $q\left(x_T\mid x_0\right)\approx \mathcal{N}(0,I)$，它将接近零。

如（Ho 等人, 2020）所述，方程 2 中定义的加噪过程允许我们直接对输入 $x_0$ 条件采样任意步骤。令 ${\alpha }_t:=1-{\beta }_t$ 和 ${\bar{\alpha }}_t:={\prod }_{s=0}^t{\alpha }_s$，我们可以写出边际：
$$q\left(x_t\mid x_0\right)=\mathcal{N}\left(x_t;\sqrt{{\bar{\alpha }}_t}{x}_0,\left(1-{\bar{\alpha }}_t\right)I\right)(8)$$
$$x_t=\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}ϵ(9)$$
其中 $ϵ\sim \mathcal{N}(0,I)$。这里，$1-{\bar{\alpha }}_t$ 告诉我们任意时间步的噪声方差，我们可以等价地使用它来定义噪声调度而不是 ${\beta }_t$。

使用贝叶斯定理，我们可以根据 ${\tilde{\beta }}_t$ 和 ${\tilde{\mu }}_t\left(x_t,x_0\right)$ 计算后验 $q\left(x_{t-1}\mid x_t,x_0\right)$，定义如下：
$${\tilde{\beta }}_t:=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}{\beta }_t(10)$$
$${\tilde{\mu }}_t\left(x_t,x_0\right):=\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}{x}_0+\frac{\sqrt{{\alpha }_t}\left(1-{\bar{\alpha }}_{t-1}\right)}{1-{\bar{\alpha }}_t}{x}_t$$
$$q\left(x_{t-1}\mid x_t,x_0\right)=\mathcal{N}\left(x_{t-1};\tilde{\mu }\left(x_t,x_0\right),{\tilde{\beta }}_{t}I\right)(12)$$

2.2 实践中的训练

方程 4 中的目标是独立项 $L_{t-1}$ 的和，方程 9 提供了一种从前向加噪过程的任意步采样的高效方法，并使用后验（方程 12）和先验（方程 3）估计 $L_{t-1}$。因此，我们可以随机采样 t 并使用期望 $E_{t,x_0,ϵ}\left[L_{t-1}\right]$ 来估计 $L_{vlb}$。Ho 等人（2020）对每个小批量中的每个图像均匀采样 t。

在先验中参数化 ${\mu }_{\theta }\left(x_t,t\right)$ 有许多不同方法。最明显的选项是用神经网络直接预测 ${\mu }_{\theta }\left(x_t,t\right)$。或者，网络可以预测 $x_0$，并使用此输出在方程 11 中产生 ${\mu }_{\theta }\left(x_t,t\right)$。网络还可以预测噪声 $ϵ$ 并使用方程 9 和 11 推导：
$${\mu }_{\theta }\left(x_t,t\right)=\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }\left(x_t,t\right)\right)(13)$$
Ho 等人（2020）发现预测 $ϵ$ 效果最好，尤其是与重新加权的损失函数结合时：
$$L_{\text{simple}}=E_{t,x_0,ϵ}\left[||ϵ-{ϵ}_{\theta }(x_t,t)|{|}^2\right](14)$$
该目标可以看作 $L_{vlb}$ 的重新加权形式（不影响 ${\Sigma }_{\theta }$ 的项）。作者发现优化这个重新加权的目标比直接优化 $L_{vlb}$ 产生更好的样本质量，并通过与生成分数匹配（Song & Ermon, 2019; 2020）的联系解释这一点。

一个微妙之处是 $L_{\text{simple}}$ 不为 ${\Sigma }_{\theta }(x_t,t)$ 提供学习信号。然而，这无关紧要，因为 Ho 等人（2020）通过将方差固定为 ${\sigma }_t^{2}I$ 而不是学习它，取得了最佳结果。他们发现使用 ${\sigma }_t^2={\beta }_t$ 或 ${\sigma }_t^2={\tilde{\beta }}_t$ 实现了相似的样本质量，这些是给定 $q(x_0)$ 为各向同性高斯噪声或 delta 函数时的方差上下界。

3 改进对数似然

虽然 Ho 等人（2020）发现 DDPM 可以根据 FID（Heusel 等人, 2017）和 Inception Score（Salimans 等人, 2016）生成高保真样本，但无法用这些模型实现竞争性的对数似然。对数似然是生成建模中广泛使用的指标，通常认为优化对数似然迫使生成模型捕获数据分布的所有模式（Razavi 等人, 2019）。此外，最近工作（Henighan 等人, 2020）表明，对数似然的微小改进可以对样本质量和学习特征表示产生巨大影响。因此，探索为什么 DDPM 在此指标上表现不佳很重要，因为这可能表明基本短板，如坏的模式覆盖。本节探索第 2 节所述算法的几个修改，这些修改结合时，允许 DDPM 在图像数据集上实现更好的对数似然，表明这些模型享有与其他基于似然的生成模型相同的好处。

为了研究不同修改的效果，我们在 ImageNet 64 $\times$ 64（van den Oord 等人, 2016b）和 CIFAR-10（Krizhevsky, 2009）数据集上训练固定模型架构和固定超参数。虽然 CIFAR-10 在此类模型中更常用，但我们选择也研究 ImageNet 64 $\times$ 64，因为它提供了多样性和分辨率之间的良好权衡，允许我们快速训练模型而无需担心过拟合。此外，ImageNet $64\times 64$ 已在生成建模背景下被广泛研究（van den Oord 等人, 2016c; Menick & Kalchbrenner, 2018; Child 等人, 2019; Roy 等人, 2020），允许我们直接比较 DDPM 与许多其他生成模型。

Ho 等人（2020）的设置（优化 $L_{\text{simple}}$，同时设置 ${\sigma }_t^2={\beta }_t$ 和 $T=1000$）在 200K 训练迭代后在 ImageNet $64\times 64$ 上实现了 3.99（比特/维度）的对数似然。在早期实验中，我们发现通过将 T 从 1000 增加到 4000 可以提升对数似然；随着此变化，对数似然改进到 3.77。在本节剩余部分，我们使用 $T=4000$，但在第 4 节探索此选择。

3.1 学习 ${\Sigma }_{\theta }(x_t,t)$

在 Ho 等人（2020）中，作者设置 ${\Sigma }_{\theta }(x_t,t)={\sigma }_t^{2}I,$，其中 ${\sigma }_t$ 未学习。奇怪的是，他们发现将 ${\sigma }_t^2$ 固定为 ${\beta }_t$ 产生与固定为 ${\tilde{\beta }}_t$ 大致相同的样本质量。

考虑到 ${\beta }_t$ 和 ${\tilde{\beta }}_t$ 代表两个极端，很自然问为什么此选择不影响样本。一个线索由图 1 提供，它显示 ${\beta }_t$ 和 ${\tilde{\beta }}_t$ 几乎相等，除了 near $t=0$，即模型处理不可感知细节时。此外，随着我们增加扩散步数，${\beta }_t$ 和 ${\tilde{\beta }}_t$ 似乎在更多扩散过程中保持彼此接近。这表明，在无限扩散步的极限下，${\sigma }_t$ 的选择可能对样本质量根本不重要。换句话说，随着我们添加更多扩散步，模型均值 ${\mu }_{\theta }(x_t,t)$ 比 ${\Sigma }_{\theta }(x_t,t)$ 更决定分布。

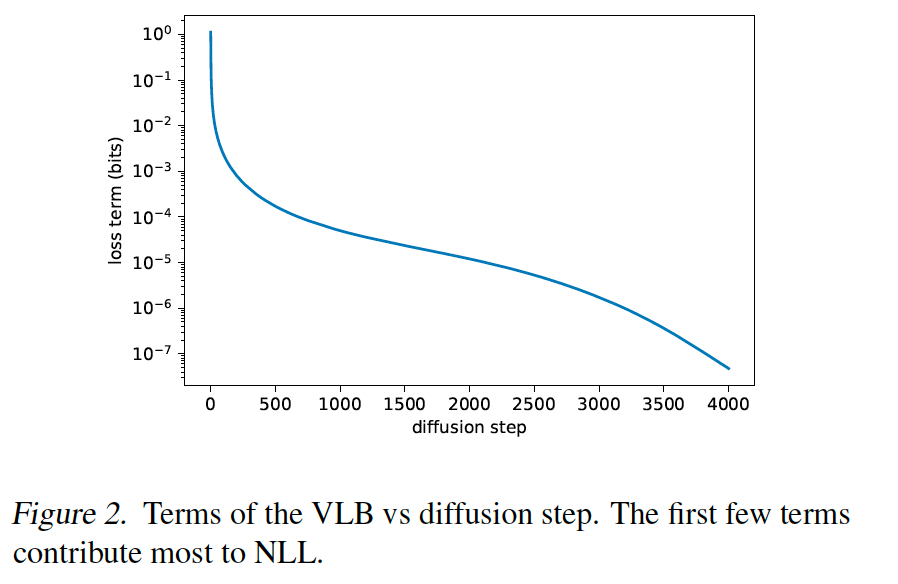
虽然上述论证表明固定 ${\sigma }_t$ 是为了样本质量的合理选择，但它未说明对数似然。实际上，图 2 显示扩散过程的前几步对变分下界贡献最大。因此，似乎可能通过使用更好的 ${\Sigma }_{\theta }(x_t,t)$ 选择来改进对数似然。为了实现这一点，我们必须学习 ${\Sigma }_{\theta }(x_t,t)$，而不遇到 Ho 等人（2020）的不稳定性。

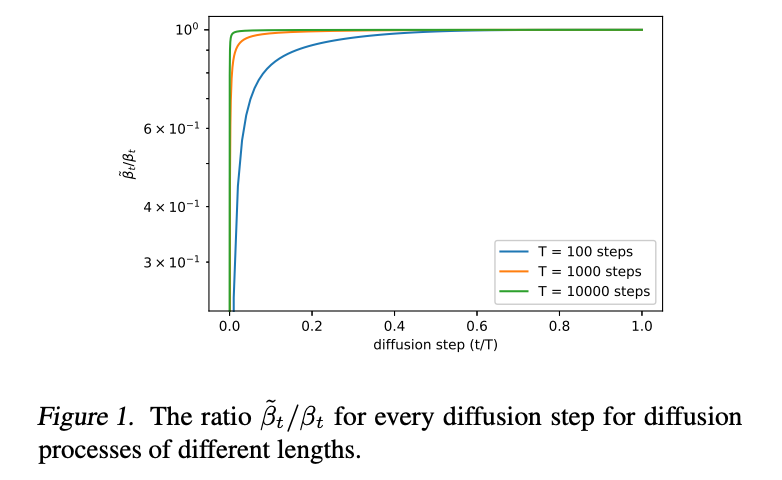
由于图 1 显示 ${\Sigma }_{\theta }(x_t,t)$ 的合理范围非常小，即使在对数域中，神经网络直接预测 ${\Sigma }_{\theta }(x_t,t)$ 也会很困难，如 Ho 等人（2020）所观察。相反，我们发现更好的是将方差参数化为 ${\beta }_t$ 和 ${\tilde{\beta }}_t$ 在对数域中的插值。具体地，我们的模型输出一个向量 v，包含每个维度的一个分量，并将此输出转换为方差如下：
$${\Sigma }_{\theta }(x_t,t)=\exp (v\log {\beta }_t+(1-v)\log {\tilde{\beta }}_t)(15)$$
我们未对$v$应用任何约束，理论上允许模型预测插值范围外的方差。然而，我们在实践中未观察到网络这样做，表明 ${\Sigma }_{\theta }\left(x_t,t\right)$ 的边界确实足够表达。

由于 $L_{\text{simple}}$ 不依赖于 ${\Sigma }_{\theta }\left(x_t,t\right)$，我们定义一个新的混合目标：
$$L_{hybrid}=L_{simple}+\lambda L_{vlb}(16)$$
对于我们的实验，我们设置 $\lambda =0.001$ 以防止 $L_{\text{vlb}}$ 压倒 $L_{\text{simple}}$。沿着同样的推理线，我们也对 $L_{\text{vlb}}$ 项的 ${\mu }_{\theta }(x_t,t)$ 输出应用停止梯度。这样，$L_{\text{vlb}}$ 可以指导 ${\Sigma }_{\theta }(x_t,t)$，而 $L_{\text{simple}}$ 仍然是 ${\mu }_{\theta }(x_t,t)$ 的主要影响源。

3.2 改进噪声调度

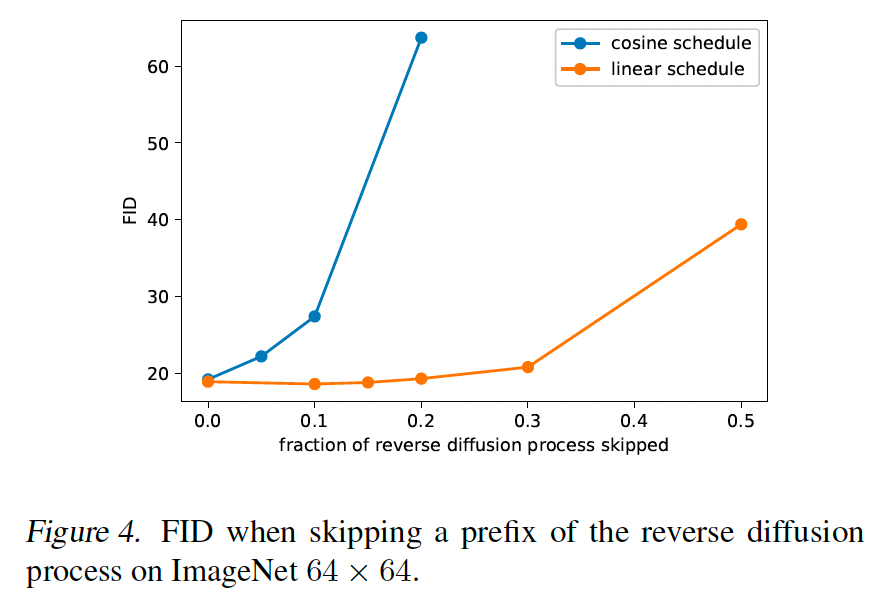
我们发现，虽然 Ho 等人（2020）中使用的线性噪声调度在高分辨率图像上工作良好，但对于 $64\times 64$ 和 $32\times 32$ 分辨率的图像是次优的。特别是，前向加噪过程的末端过于嘈杂，因此对样本质量贡献不大。这可以在图 3 中视觉看到。

此效果的结果在图 4 中研究，我们看到当跳过反向扩散过程的前缀高达 $20\%$ 时，使用线性调度训练的模型不会变差太多（按 FID 测量）。

为了解决此问题，我们根据 ${\bar{\alpha }}_t$ 构建一个不同的噪声调度：
$$\begin{array}{r}{\bar{\alpha }}_t=\frac{f(t)}{f(0)},f(t)=\cos {\left(\frac{t/T+s}{1+s}\cdot \frac{\pi }{2}\right)}^2\end{array}(17)$$
为了从此定义到方差 ${\beta }_t$，我们注意 ${\beta }_t=1-\frac{{\bar{\alpha }}_t}{{\bar{\alpha }}_{t-1}}$。实践中，我们将 ${\beta }_t$ 裁剪到不大于 0.999，以防止在扩散过程末端 near $t=T$ 出现奇点。

我们的余弦调度设计为在过程中间具有 ${\bar{\alpha }}_t$ 的线性下降，同时在 $t=0$ 和 $t=T$ 的极端附近变化很小，以防止噪声水平的突然变化。图 5 显示两种调度下 ${\bar{\alpha }}_t$ 的进展。我们可以看到 Ho 等人（2020）的线性调度更快地下降到零，比必要更快地破坏信息。

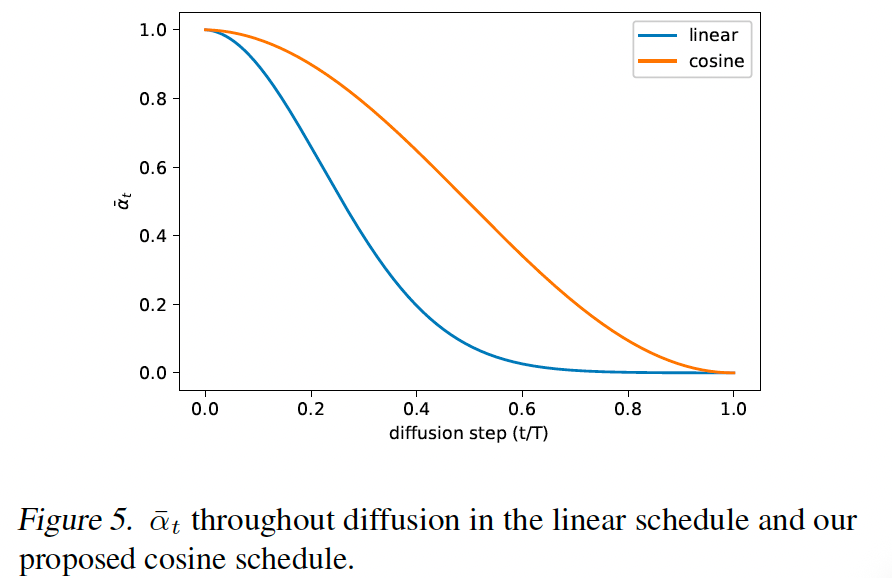
我们使用一个小偏移 $s$ 以防止 ${\beta }_t$ 在 $t=0$ 附近太小，因为我们发现在过程开始时有微量噪声使网络难以足够准确地预测 $e$。具体地，我们选择 $s$ 使得 $\sqrt{{\beta }_0}$ 略小于像素桶大小 1/127.5，这给出 $s$= 0.008。我们选择使用 cos² 特别是因为它是一个常见的数学函数，具有我们寻找的形状。此选择是任意的，我们期望许多其他具有相似形状的函数也会工作。

3.3 减少梯度噪声

我们期望通过直接优化 $L_{\text{vlb}}$ 而不是优化 $L_{\text{hybrid}}$ 实现最佳对数似然。然而，我们惊讶地发现 $L_{vlb}$ 在实践中相当难优化，至少在高多样性的 ImageNet 64x64 数据集上。图 6 显示 $L_{vlb}$ 和 $L_{hybrid}$ 的学习曲线。两条曲线都有噪声，但混合目标在相同训练时间下在训练集上明显实现更好的对数似然。

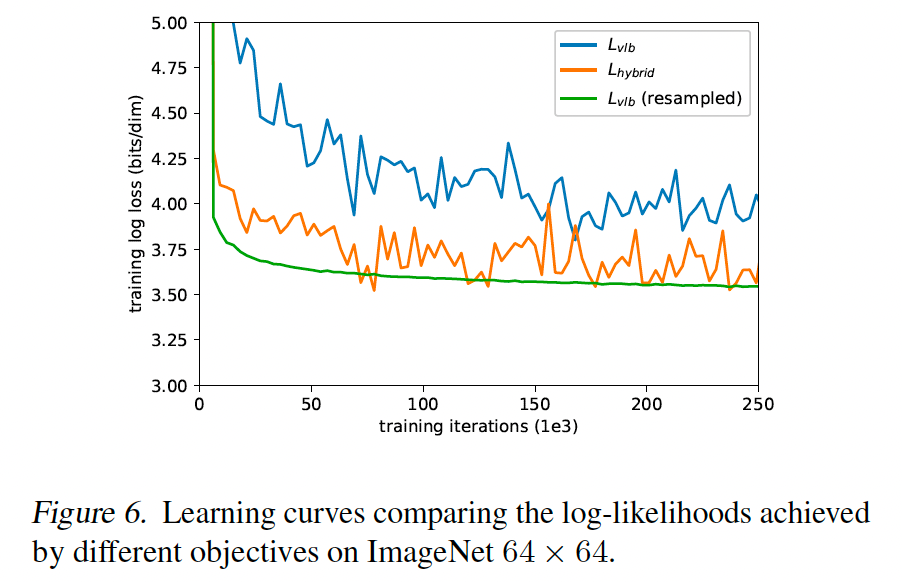
我们假设 $L_{vlb}$ 的梯度比 $L_{hybrid}$ 的梯度噪声大得多。我们通过评估用两个目标训练的模型的梯度噪声尺度（McCandlish 等人, 2018）来确认这一点，如图 7 所示。因此，我们寻求一种减少 $L_{\text{vlb}}$ 方差的方法，以便直接优化对数似然。

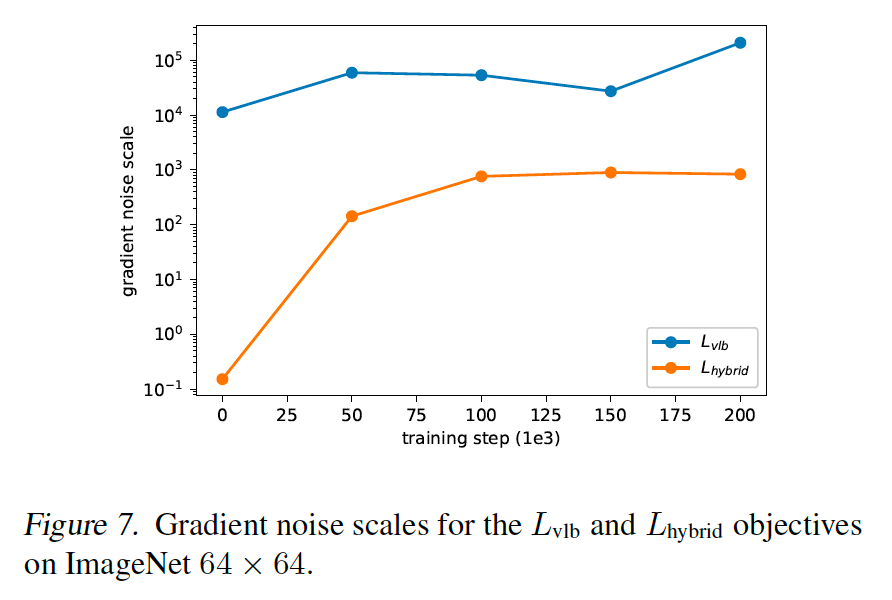
注意到 $L_{\text{vlb}}$ 的不同项具有非常不同的量级（图 2），我们假设均匀采样 t 导致 $L_{\text{vlb}}$ 目标中不必要的噪声。为了解决此问题，我们采用重要性采样：
$L_{\text{vlb}}=E_{t\sim p_t}\left[\frac{L_t}{p_t}\right]$，其中 $p_t\propto \sqrt{E[L_t^2]}$ 且 $\sum p_t=1$
由于 $E\left[L_t^2\right]$ 事先未知并在训练过程中可能改变，我们维护每个损失项之前 10 个值的历史，并在训练期间动态更新。在训练开始时，我们均匀采样 t，直到我们为每个 $t\in [0,T-1]$ 抽取 10 个样本。

使用此重要性采样目标，我们能够通过优化 $L_{vlb}$ 实现最佳对数似然。这可以在图 6 中看到，作为 Lvlb（重采样）曲线。图还显示重要性采样目标比原始均匀采样目标噪声小得多。我们发现重要性采样技术在直接优化噪声较小的 Lhybrid 目标时没有帮助。

3.4 结果与消融研究

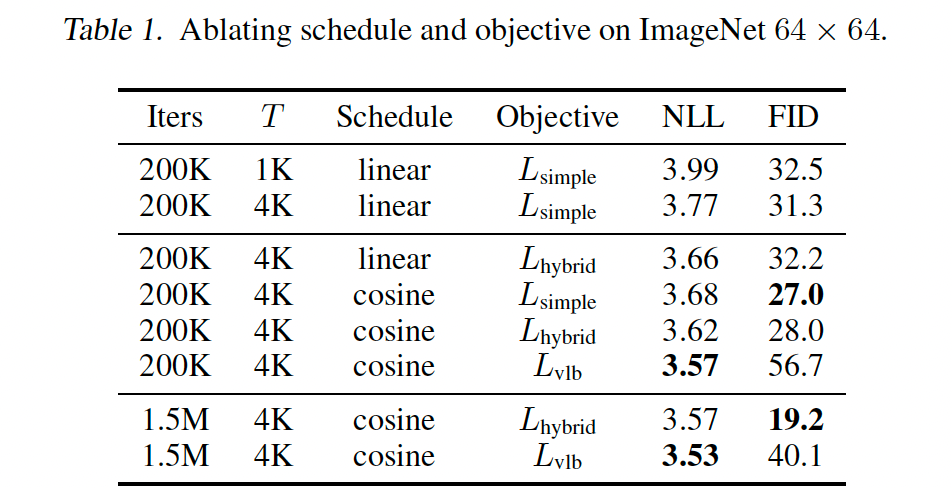
在本节中，我们消融我们为实现更好对数似然而做的修改。表 1 总结了我们在 ImageNet 64 x 64 上的消融结果，表 2 显示了 CIFAR-10 的结果。我们还训练了我们最好的 ImageNet 64 x 64 模型 1.5M 迭代，并报告这些结果。$L_{\text{vlb}}$ 和 $L_{\text{hybrid}}$ 使用第 3.1 节的参数化与学习 sigma 训练。对于 $L_{\text{vlb}}$，我们使用了第 3.3 节的重采样方案。

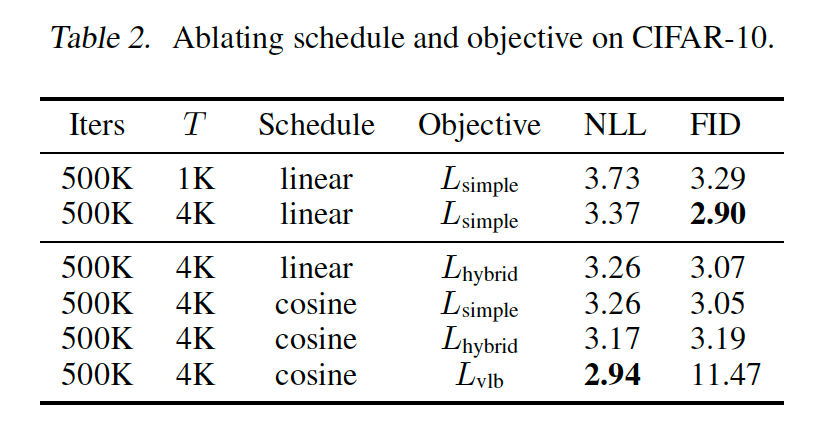
基于我们的消融，使用 $L_{\text{hybrid}}$ 和我们的余弦调度改进对数似然，同时保持与 Ho 等人（2020）基线相似的 FID。优化 $L_{\text{vlb}}$ 进一步改进对数似然，但代价是更高的 FID。我们通常更喜欢使用 $L_{\text{hybrid}}$ 而不是 $L_{\text{vlb}}$，因为它在不牺牲样本质量的情况下提升似然。

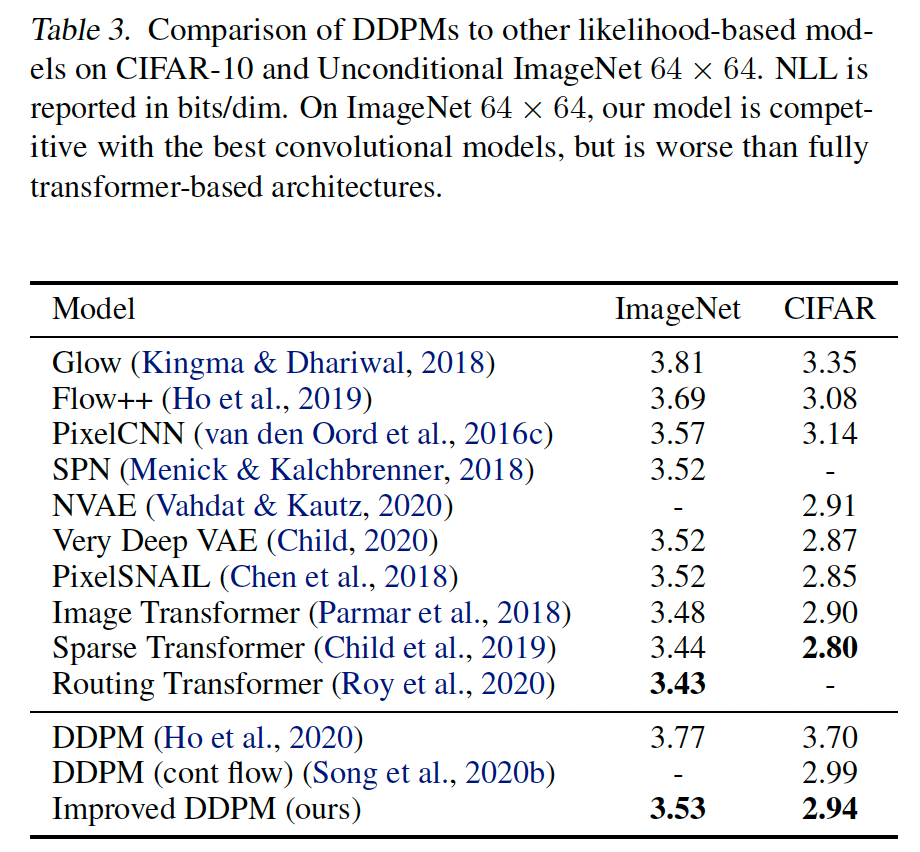
在表 3 中，我们比较我们最好的似然模型与先前工作，显示这些模型在对数似然方面与最佳传统方法竞争。

4 改进采样速度

我们所有的模型都用 4000 个扩散步训练，因此在现代 GPU 上产生单个样本需要几分钟。在本节中，我们探索如果减少采样期间使用的步数，性能如何缩放，并发现我们预训练的 Lhybrid 模型可以用比训练时少得多的扩散步产生高质量样本（无需任何微调）。以这种方式减少步数使得在几秒而不是几分钟内从我们的模型采样成为可能，并大大提高了图像 DDPM 的实际适用性。

对于用 T 个扩散步训练的模型，我们通常使用与训练期间相同的 t 值序列（1,2,…,T）进行采样。然而，也可以使用 t 值的任意子序列 S 进行采样。给定训练噪声调度$a$，对于给定序列 S，我们可以获得采样噪声调度 ${\bar{\alpha }}_{S_t}$，然后可以用于获得相应的采样方差：
$$\begin{array}{r}{\beta }_{S_t}=1-\frac{{\bar{\alpha }}_{S_t}}{{\bar{\alpha }}_{S_{t-1}}},{\tilde{\beta }}_{S_t}=\frac{1-{\bar{\alpha }}_{S_{t-1}}}{1-{\bar{\alpha }}_{S_t}}{\beta }_{S_t}\end{array}(19)$$
现在，由于 ${\Sigma }_{\theta }(x_{S_t},S_t)$ 被参数化为 ${\beta }_{S_t}$ 和 ${\tilde{\beta }}_{S_t}$ 之间的范围，它将自动为较短的扩散过程重新缩放。因此我们可以计算 $p(x_{S_{t-1}}|x_{S_t})$ 为 $$\mathcal{N}({\mu }_{\theta }(x_{S_t},S_t),{\Sigma }_{\theta }(x_{S_t},S_t)).$$

为了将采样步数从 $T$减少到 $K$，我们使用 1 到 $T$（含）之间均匀间隔的 $K$ 个实数，然后将每个结果数字四舍五入到最接近的整数。

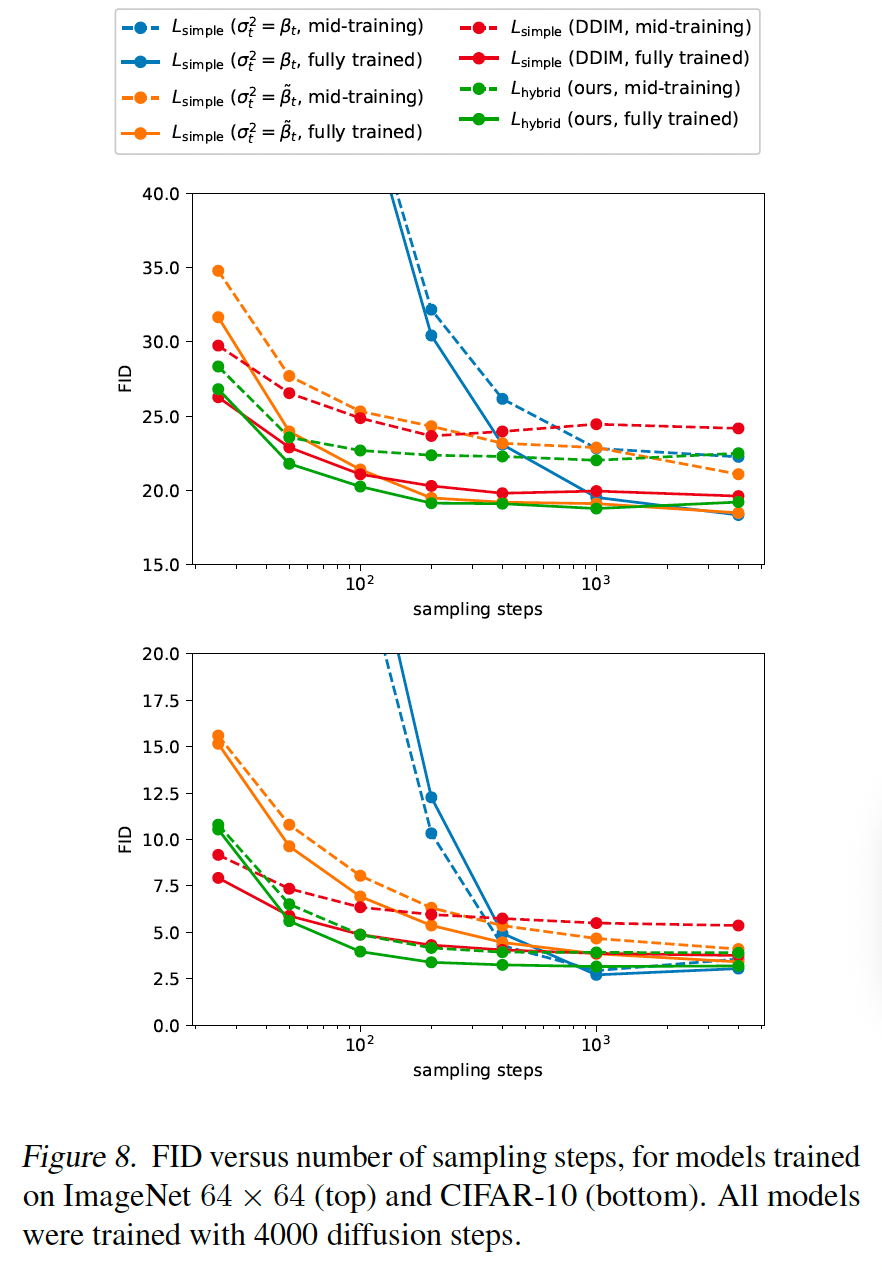
在图 8 中，我们评估了一个 Lhybrid 模型和一个用 4000 个扩散步训练的 $L_{\text{simple}}$ 模型的 FID，使用 25、50、100、200、400、1000 和 4000 个采样步。我们对完全训练的检查点和训练中途的检查点都这样做。对于 CIFAR-10，我们使用 200K 和 500K 训练迭代，对于 ImageNet-64，我们使用 500K 和 1500K 训练迭代。我们发现具有固定 sigma 的 Lsimple 模型（使用较大的 ${\sigma }_t^2={\beta }_t$ 和较小的 ${\sigma }_t^2={\tilde{\beta }}_t$）在使用减少的采样步数时样本质量下降更多，而我们具有学习 sigma 的 Lhybrid 模型保持高样本质量。使用此模型，100 个采样步足以实现我们完全训练模型的近最优 FID。

与我们的工作并行，Song 等人（2020a）通过产生一个新的隐式模型提出了一种 DDPM 的快速采样算法，该模型具有相同的边际噪声分布，但确定性地将噪声映射到图像。我们在图 8 中包含了他们的算法 DDIM，发现 DDIM 在使用少于 50 个采样步时产生更好的样本，但使用 50 个或更多步时产生更差的样本。有趣的是，DDIM 在训练开始时表现更差，但随着训练继续缩小与其他采样器的差距。我们发现我们的跨步技术大大降低了 DDIM 的性能，因此我们的 DDIM 结果改用 Song 等人（2020a）的常数跨步，其中最终时间步是 T-T/K+1 而不是 T。其他采样器用我们的跨步表现稍好。

5 与 GANs 的比较

虽然似然是模式覆盖的好代理，但用此指标与 GAN 比较是困难的。相反，我们转向精确率和召回率（Kynkanniemi 等人, 2019）。由于在 GAN 文献中训练类条件模型很常见，我们为此实验也这样做。为了使我们的模型类条件，我们通过与时间步 t 相同的路径注入类信息。具体地，我们将类嵌入 $v_i$ 添加到时间步嵌入 $e_t$，并将此嵌入传递给整个模型中的残差块。我们使用 Lhybrid 目标训练，并使用 250 个采样步。我们训练两个模型：一个“小”模型，具有 1 亿参数，训练 1.7M 步；一个更大的模型，具有 2.7 亿参数，训练 250K 迭代。我们训练一个 BigGAN-deep 模型，生成器和判别器共有 1 亿参数。

当计算此任务的指标时，我们生成了 50K 样本（而不是 10K）以直接与其他工作可比。这是唯一使用 50K 样本计算的 ImageNet $64\times 64$ FID。对于 FID，参考分布特征是在完整训练集上计算的，遵循 Brock 等人（2018）。

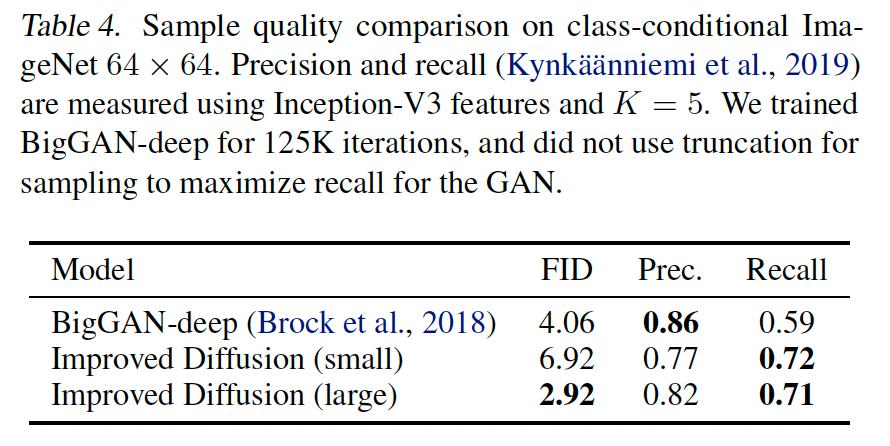
图 9 显示了我们较大模型的样本，表 4 总结了我们的结果。我们发现 BigGAN-deep 在 FID 方面优于我们较小的模型，但在召回率方面挣扎。这表明扩散模型在覆盖分布模式方面比可比的 GAN 更好。

6 缩放模型大小

在前几节中，我们展示了在不改变训练计算量的情况下改进对数似然和 FID 的算法变化。然而，现代机器学习的一个趋势是更大的模型和更多的训练时间往往会提高模型性能（Kaplan 等人, 2020; Chen 等人, 2020a; Brown 等人, 2020）。给定此观察，我们研究 FID 和 NLL 如何作为训练计算量的函数缩放。我们的结果虽然是初步的，但表明 DDPM 随着训练计算量的增加以可预测的方式改进。

为了测量性能如何随训练计算量缩放，我们在 ImageNet 64 x 64 上训练四个不同的模型，使用第 3.1 节描述的 Lhybrid 目标。为了改变模型容量，我们在所有层应用深度乘数，使得第一层有 64、96、128 或 192 个通道。注意我们之前的实验在第一层使用 128 个通道。由于每层的深度影响初始权重的尺度，我们按 1/√通道乘数缩放每个模型的 Adam（Kingma & Ba, 2014）学习率，使得 128 通道模型的学习率为 0.0001（如我们其他实验）。

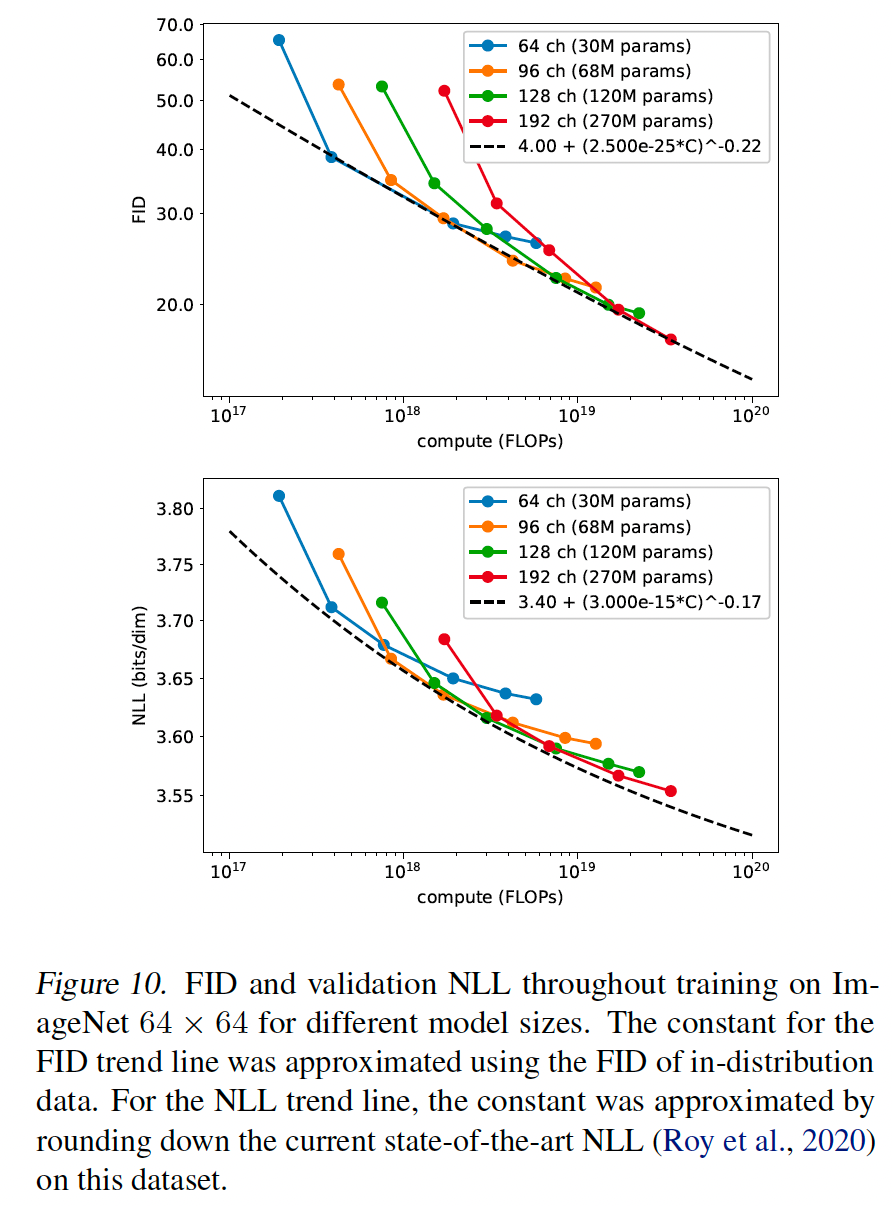
图 10 显示 FID 和 NLL 如何相对于理论训练计算量改进。FID 曲线在 log-log 图上看起来近似线性，表明 FID 根据幂律缩放（绘制为黑色虚线）。NLL 曲线不那么贴合幂律，表明验证 NLL 以不太有利的方式缩放。

7 相关工作

Chen 等人（2020b）和 Kong 等人（2020）是最近使用 DDPM 产生基于 mel 频谱图的条件高保真音频的两个工作。与我们的工作同时，Chen 等人（2020b）使用改进的调度和 L1 损失的组合，允许以很少的样本质量减少用更少的步采样。然而，与我们的无条件图像生成任务相比，他们的生成任务有由 mel 频谱图提供的强输入条件信号，我们假设这使得用更少的扩散步采样更容易。

Jolicoeur-Martineau 等人（2020）探索了图像域中的分数匹配，并构建了一个对抗训练目标以产生更好的 x0 预测。然而，他们发现选择更好的网络架构移除了对此对抗目标的需要，表明对抗目标对于强大的生成建模不是必要的。

与我们的工作并行，Song 等人（2020a）和 Song 等人（2020b）通过利用不同的采样过程提出了用 DDPM 目标训练的模型的快速采样算法。Song 等人（2020a）通过推导一个隐式生成模型来实现这一点，该模型具有与 DDPM 相同的边际噪声分布，同时确定性地将噪声映射到图像。Song 等人（2020b）将扩散过程建模为连续 SDE 的离散化，并观察存在一个对应于从反向 SDE 采样的 ODE。通过改变 ODE 求解器的数值精度，他们可以用更少的函数评估采样。然而，他们指出此技术直接使用时比祖先采样获得更差的样本，并且仅当与 Langevin 校正器步结合时才实现更好的 FID。这又需要手动调整 Langevin 步的信噪比。我们的方法允许直接从祖先过程快速采样，这消除了对额外超参数的需要。

Also in parallel, Gao 等人（2020）开发了一个扩散模型，其反向扩散步由基于能量的模型建模。此方法的一个潜在含义是应该需要更少的扩散步来实现好样本。

8 结论

我们已经表明，通过一些修改，DDPM 可以采样更快，并实现更好的对数似然，而对样本质量影响很小。似然通过使用我们的参数化和 $L_{hybrid}$ 目标学习 ${\Sigma }_{\theta }$ 得到改进。这使这些模型的似然更接近其他基于似然的模型。我们惊讶地发现此变化也允许用少得多的步从这些模型采样。

我们还发现 DDPM 可以匹配 GAN 的样本质量，同时实现更好的模式覆盖（按召回率测量）。此外，我们研究了 DDPM 如何随可用训练计算量缩放，并发现更多的训练计算量轻松导致更好的样本质量和对数似然。

这些结果的结合使 DDPM 成为生成建模的有吸引力选择，因为它们结合了好的对数似然、高质量样本和相当快的采样，以及一个基于良好的、平稳的训练目标，该目标随训练计算量轻松缩放。这些结果表明 DDPM 是未来研究的有希望方向。

转载自CSDN-专业IT技术社区

原文链接：https://blog.csdn.net/qq_34941290/article/details/157937605